Essence of Albert Einstein's Resolution of the Twin Paradox (from Dialog about Objections against the Theory of Relativity, 1918) [1] [2] [3]
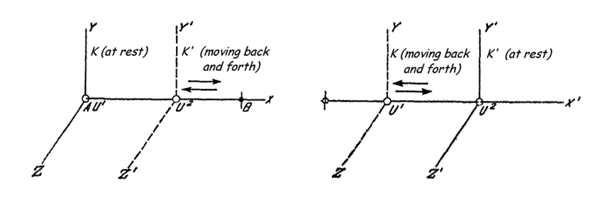
Let K be a Galilean coordinate system in the sense of the special theory of relativity, that is, a frame of reference, relative to which isolated, material points move in straight lines and uniformly. Also, let U1 and U2 be two identical clocks that are free from outside influences.
Let A and B be two distant points of the system K. To render the picture more precise, let A be the origin of K, and B be a point on the positive x-axis. The two clocks are initially at rest at point A. They run at the same pace, and let the positions of the hands be the same. We now impart to clock U2 a constant velocity in the positive direction of the x-axis, so that it moves towards B. At B we imagine the velocity reversed, so that clock U2 returns to A. As it arrives at A, the clock is decelerated so that it is once again at rest relative to U1.
It is certainly correct that from the point of view of the general theory of relativity we can just as well use coordinate system K' [co-moving with clock U2] as coordinate system K. But it is easy to see that the systems K and K' in connection with the examined proceedings stand by no means on equal footing:
According to both descriptions the clock U2 is running a certain amount behind clock U1 at the end of the observed process. When relating to the coordinate system K' the behavior explains itself as follows: During the partial processes 2 and 4 the clock U1, going at a velocity v, runs indeed at a slower pace than the [in K'] resting clock U2. However, this is more than compensated by a faster pace of U1 during partial process 3. According to the general theory of relativity, a clock will go faster the higher [weaker] the gravitational potential of the location where it is located, and during partial process 3 U2 happens to be located at a higher [weaker] gravitational potential than U1. The calculation shows that this speeding ahead constitutes exactly twice as much as the lagging behind during the partial processes 2 and 4.
[1] This is a summary of Einstein's resolution of the twin paradox of 1918. The summary is compiled from extracts of the Wikisource translation of Einstein's Dialog über Einwände gegen die Relativitätstheorie.
[2] C. S. Unnikrishnan published in 2005 a paper On Einstein’s resolution of the twin clock paradox. A quote from the abstact:
"Einstein addressed the twin paradox in special relativity in a relatively unknown, unusual and rarely cited paper written in 1918, in the form of a dialogue between a critic and a relativist. Contrary to most textbook versions of the resolution, Einstein admitted that the special relativistic time dilation was symmetric for the twins, and he had to invoke, asymmetrically, the general relativistic gravitational time dilation during the brief periods of acceleration to justify the asymmetrical aging. Notably, Einstein did not use any argument related to simultaneity or Doppler shift in his analysis. I discuss Einstein’s resolution and several conceptual issues that arise. It is concluded that Einstein’s resolution using gravitational time dilation suffers from logical and physical flaws, and gives incorrect answers in a general setting."
[3] I've compiled this summary for use in a debate over time
dilation and twin paradox. Unnikrishnan's conclusion is confirmed also by my
examination: The grand finale of Einstein's resolution of the twin paradox is so
full of logical, physical and mathematical flaws that it can only be
explained by excessive demand, psychological stress and wishful thinking.